Saptamana trecuta am cerut intr-un magazin un sfert dintr-o "roata" de branza. Am primit o bucata care arata ca mai jos:


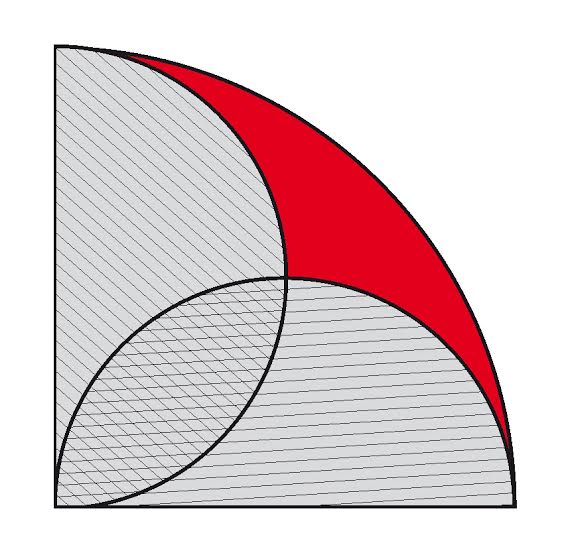
Totusi, un sfert de cerc face un unghi drept in punctul intersectarii razelor care il delimiteaza. Arata ca in figura de mai jos. Daca pe cele doua raze construim cate un semicerc care sa aiba centrul diametrului in centrul razei, obtinem patru suprafete care arata ca in figura de mai jos. Se cere sa se determine, fara prea multe calcule (si fara hartie si creion, daca se poate) care este raportul dintre suprafata dublu hasurata (intersectia semicercurilor) si suprafata colorata in rosu.
Doi melci se antreneaza impreuna pentru o cursa de semifond. Performantele lor sunt egale, atat la alergarea usoara, cat si la viteza. Insa pentru cursa cei doi isi stabilesc strategia diferit. Primul o sa alerge incet in prima jumatate a distantei si repede in a doua jumatate. Cel de-al doilea o sa alerge repede in prima jumatate a duratei si incet in a doua. Putem sti dinainte care dintre ei o sa castige cursa?
- Rezolvari
Cercul
Cele doua suprafete sunt egale. Semicercurile alcatuiesc un cerc cu o suprafata egala cu a sfertului de cerc de la care am pornit constructia (raza lor este jumatate din raza cercului initial). Prin urmare, suma lor din care scadem suprafata de intersectie si adunam suprafata colorata este egala cu suprafata sfertului de cerc. Altfel spus, daca notam cu S suprafata sfertului de cerc, cu H1 si H2 suprafetele semicercurilor, cu R suprafata colorata in rosu si cu X suprafata de intersectie a semicercurilor, avem relatia R = S - H1 - H2 + X. Cum S = H1 + H2, rezulta R = X.
Melcii
Castigator o sa fie melcul care si-a ales ca punct de schimbare a vitezelor jumatatea duratei. Daca luam separat cursa fiecarui melc si o impartim in doua dupa punctul de schimbare a vitezelor, o sa vedem ca primul melc alearga repede jumatate din distanta cursei, in vreme ce al doilea alearga repede mai putin de jumatate (fiindca alearga repede tot atat timp cat alearga incet, deci distantele acoperite in cele doua jumatati sunt diferite). Rezulta ca al doilea strateg o sa treaca linia de sosire mai devreme decat primul.
- Mentiuni
Problemele de data trecuta au fost cele mai usoare. Una dintre ele chiar a primit o medie a notelor de sub 1 din 5. Asta inseamna ca legenda creata in jurul ei (care spune ca peste 80% dintre raspunsuri sunt gresite) nu e valabila pentru cititorii acestei rubrici, ceea ce e imbucurator.
Le multumesc tuturor celor care au trimis raspunsuri si notari, si mai ales celorcare au avut rabdarea de a trece peste eroarea comisa la redactarea primei probleme. Din pacate nu avem niciun castigator de premii. Sper ca aceasta situatie o sa ramana unica.
NB: I-as ruga pe cei care imi trimit rezolvari prin e-mail sa spuna si cat de grea li se pare problema la care raspund (pe o scara de la 1 la 5). Multumesc. Comentariile, intrebarile, propunerile, sugestiile si reclamatiile sunt asteptate la viorel.zaicu@hotnews.ro.
Editura Paralela 45 sponsorizeaza ganditorii cu doua titluri in fiecare saptamana: Boris Kordemski, 359 de probleme de matematica recreativa, si Martin Gardner, Cele mai indragite jocuri matematice si logice. Premiile sunt oferite cititorilor care fie ofera o solutie originala (sau o explicatie simpla si inedita) la problemele date, fie propun o problema pe care n-am mai intalnit-o (cel putin nu in varianta respectiva). Nu va straduiti sa fiti originali cu orice pret - daca sunt mai multi castigatori o sa fie si mai multe carti!
- Nota redactiei: Comentariile la acest articol vor fi publicate duminica, odata cu publicarea rezolvarilor.
Cititi si provocarile de logica din saptamanile trecute:
Un calugar si trei maestri ai logicii
Cartofii-minune si pastilele salvatoare
Guguta, ciorba si puntea afurisita
O cada de baie si 10 logicieni