Provocarea de logica a saptamanii: Guguta, ciorba si puntea afurisita (UPDATE cu rezolvarile)

Viorel Zaicu • HotNews.ro

Guguta are trei borcane. Unul tine 800 ml de ciorba si e plin, altul 500 (si e gol), iar cel mai mic - 300 (si e tot gol). Pe Guguta il roaga soata sa ii imparta ciorba in doua portii de cate 400 ml. De asemenea, ii cere sa n-o vanture prea mult. Cam cum ar putea Guguta sa faca asta?

Anunt: Incepand de astazi am posibilitatea sa ofer cateva premii in carti. Editura Paralela 45 sponsorizeaza ganditorii cu doua titluri in fiecare saptamana: Boris Kordemski, 359 de probleme de matematica recreativa, si Martin Gardner, Matematica recreativa. Primul volum o sa mearga la cititorul care ofera o solutie originala (sau o explicatie simpla si inedita) la problemele date, iar cel de-al doilea o sa ajunga la cititorul care propune o problema pe care n-am mai intalnit-o (cel putin nu in varianta pe care o propune dumnealui). Nu va straduiti sa fiti originali cu orice pret - daca sunt mai multi castigatori o sa fie si mai multe carti!

Dupa ce a impartit ciorba exact cum i s-a cerut, Guguta da de alt necaz...

Impreuna cu soata si socrii trebuie sa traverseze un hau peste o punte ingusta, noaptea. Puntea este si cam subreda, asa ca pe ea nu se pot afla niciodata mai mult de doua persoane. Nu au decat un felinar, care trebuie sa se afle de fiecare data la una dintre persoanele care traverseaza, altfel pe punte nu se poate face vreun pas. Socrul lui Guguta poate trece puntea in 8 minute, iar el in 1. Soacra are nevoie de 7 minute, iar sotia lui Guguta - de 2. Pot trece toti puntea in 15 minute?

Daca nu va plac incurcaturile lui Guguta, puteti incerca varianta americana de mai jos. Sunt chiar curios daca i se pare cuiva mai usor de rezolvat. (Mie mi se pare ca aceasta varianta contine un indiciu destul de generos...)

Patru oameni trebuie sa prinda autobuzul, care pleaca in 60 de minute. Ca sa ajunga la el trebuie sa traverseze o punte ingusta, care nu tine decat doua persoane. E noapte si au o singura lanterna, asa ca daca trec doi, unul trebuie sa se intoarca, pentru a le aduce lanterna celor ramasi. Cei patru sunt mai atleti sau mai fricosi...

Unul poate trece puntea in 5 minute, al doilea in 10, al treilea in 20 si al patrulea in 25.

Cum fac cei patru sa prinda autobuzul?

Mentiuni

Adrian Iordache, Radu Danaila si Alexandru Gosa au furnizat niste raspunsuri originale la problema cu cada - chiar daca toate erau reductibile la acelasi calcul matematic -, demonstrand ca gandirea antrenata se poate lipsi de formule. Majoritatea celor care au raspuns au tinut cont de rugamintea mea si au notat gradul de dificultate al problemei. De unde a rezultat ca problema cu logicienii a fost cea mai grea de pana acum (3 din 5).

NB: I-as ruga pe cei care imi trimit rezolvari prin e-mail sa spuna cat de grea li se pare problema la care raspund (pe o scara de la 1 la 5). Multumesc. Comentariile, intrebarile, propunerile, sugestiile si reclamatiile sunt asteptate la viorel.zaicu@hotnews.ro.

Rezolvari

Ciorba

Ciorba

Foto: Hotnews

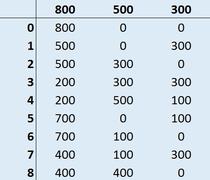
Exista o varianta cu doar 8 permutari. Ar trebui sa fie evident ca primele doua sunt umplerea borcanului de 300 si turnarea continutului in borcanul de 500. Abia de aici incolo se complica lucrurile. Daca umplem din nou borcanul de 300 si din el turnam ciorba in cel de 500 pana cand acesta se umple, apoi golim borcanul de 500 in cel mare, avem 700 ml de ciorba in borcanul mare si 100 in cel mic. Iar de aici cred ca oricine se descurca singur. Pentru cei care nu se descurca, mai jos este un tabel care descrie simplu toti pasii.

Puntea

Ambele variante ale problemei se construiesc pe un principiu simplu: timpul in care cei patru trebuie sa traverseze este atat de scurt incat este obligatoriu ca cei care traverseaza incet sa treaca amandoi odata! (In felul acesta putem "ingropa" 20 de minute in 25 sau 7 minute in 8, truc pe care se bazeaza problema. Orice alta combinatie ne face sa depasim limita.) Prin urmare, primii trec Guguta cu soata, apoi unul dintre ei se intoarce (nu are importanta care, fiindca operatiunea se va repeta) cu felinarul si trec socrii lui Guguta, care predau felinarul, iar cel aflat dincolo traverseaza inapoi si isi recupereaza partenerul. Avem doua combinatii:

2 + 2 +8 + 1 + 2 = 15

2 + 1 + 8 + 2 + 2 = 15.

In acelasi fel, la "versiunea americana" avem combinatiile:

10 + 10 + 25 + 5 + 10 = 60

10 + 5 + 25 + 10 + 10 = 60.

Cititi si:

Provocarea de logica a saptamanii: O cada de baie si 10 logicieni

Provocarea de logica a saptamanii: ￢Becuri si viteze

Provocarea de logica a saptamanii: Bile, piulite si lacate

Provocarea de logica a saptamanii: Apa si banii

Provocarea de logica a saptamanii: Herr Casanova

Provocarea de logica a saptamanii : Fitiluri si clepsidre

Provocarea de logica a saptamanii: Inviorati-va neuronii cu problema lui Einstein

RECOMANDĂRI HotNews.ro

INVESTIGAȚIE Banii big farma ajung la societatea medicală condusă de ministrul Rafila prin firma unui fost șef al spitalului SRI

Catiusa Ivanov si Radu Mihaiu in studiul HotNews.ro

VIDEO Primarul Radu Mihaiu: „Să-și cumpere câte mașini vrea, însă nu e responsabilitatea statului să-i asigure loc de parcare pentru fiecare mașină”

fanatik.ro: Deținutul periculos care a evadat la începutul lunii aprilie, bătut în închisoare. Agresorul a fost achitat

Programul Școala de Bani din Bibliotecă: peste 4.300 de copii și adulți au învățat, în ultimul an, despre bani prin intermediul a 90 de...

lovedeco.ro: De la oraș la sat: un tată și fiica lui au renovat o casă șubredă și o șură veche de 100 ani

Alianța pentru Unirea Românilor (AUR) - imagine generică

EXCLUSIV. Directivă PNL pentru toți șefii din județe: Solicitați respingerea Alianței AUR la Birourile electorale! / Ce au descoperit

Medic român întors din Franța: „Mă întreb câți medici există în Europa atât de bogați precum dr. Cîrstoiu. Doctori buni pleacă scârbiți în străinătate”

Bombă ghidată de mare precizie Paveway IV

Marea Britanie va trimite un „cadou” special forțelor aeriene ucrainene / Ce se știe despre Paveway, o armă de ultimă generație - VIDEO

„Gângăniile” electronice fără care nu ai avea telefon, mașină sau televizor. Cum arată piața de sute de miliarde de dolari care învârte lumea

panorama.ro: „Gângăniile” electronice fără care nu ai avea telefon, mașină sau televizor. Cum arată piața de sute de miliarde de dolari care învârte lumea

Testul care îți arată cât de rezistent e creierul tău. Neurochirurg: „Este o paradigmă revoluționară în domeniul sănătății creierului“. Află-ți scorul

smartliving.ro: Testul care îți arată cât de rezistent e creierul tău. Neurochirurg: „Este o paradigmă revoluționară în domeniul sănătății...

De ce grecii și spaniolii îi invidiază pe români pentru viteza internetului

„Poligon militar, loc de gunoaie și casă a migranților” - mesajul lui Șor, de la Moscova, contra referendumului Moldovei pentru UE. Analist: „Sunt...

ADAUGĂ COMENTARIU (16 comentarii)

CristianBica • 2016-04-23 13:50

Borcane // Fiecare cifra reprezintă numărul de sute de ml din fiecare borcan (in ordinea descrescătoare a borcanelor) 800 350 323 620 602 152 143 440

Serban Eduard • 2016-04-23 14:35

Rezolvare // Problema lui Guguta si cele trei borcane: Daca notam cu tripletul (a,b,c) capacitatile celor 3 borcane avem pana acum: a + b + c = 800; a<=800, b<=300, c<= 500; Inital a = 800. Avem urmatoarele transformari: (800,0,0) -> se varsa din 800 in 500 -> (300,0,500) -> se varsa din 500 in 300 -> (300,300,200) ->se varsa din b in a si avem -> (600,0,200) --> se varsa din c in b --> (600,200,0) --> de varsa cei 600 in c --> (100,200,500) si acum din c in b --> (100,300,400) si acum se insumeaza in a --> (400,0,400) Problema trecerii puntii cu soacra si socrul : Este o problema clasica in computer science intalnita la planificatorul de procese in sistemele de operare: Ideea ca cei ce merg apropiati sa mearga impreuna: Voi desena schematic: 1) Traverseaza sotul si sotia de pe malul A --> B timp 2 minute 2) Se intoarce Goguta pe malul A --> timp 1 minute 3) Traverseaza socrii impreuna de pe A in B --> timp 8 minute 4) traverseaza sotia de pe B in A singura --> 2 minute 5) traverseaza inapoi de pe A in B sotii -> 2 minute insumand timpii --> 2 + 1 +8 + 2 +2 = 15 minute La fel problema a treia identica: 1) Trec cei cu 5 minute si 10 minute podul --> durata 10 minute 2) Trece inapoi cel cu 5 minute pentru lanterna --> durata 5 minute 3) trec cei cu 10 si 25 minute -> durata 25 minute 4) trece inapoi cel cu 10 minute --> durata 10 minute 5) trec inapoi in final cel cu 5 si 10 minute --> durata 10 minute timp total: 10+5+25+10+10 = 60 minute Observatie: toate cele 3 probleme le consider probleme cu grad mediu de dificultate: punctaj 3

racing • 2016-04-23 14:46

Rezolvare // 1. Din borcanul 1 de 800 se umple borcanul 2 de 500. Raman 300 2. Din borcanul 2 de 500 se umple borcanul 3 de 300. Raman 200 in borcanul 2 3. Din borcanul 3 se transfera 300 in borcanul 1 unde vom avea 600. Borcanul 3 va fi gol. 4. Din borcanul 2 transferam 200 ramasi in borcanul 3. Borcanul 2 va fi gol. 5. Din borcanul 1 transferam 500 in borcanul 2. In borcanul 1 raman 100 6. Din borcanul 2 transferam 100 in borcanul 3 care se va umple. Borcanul 2 va avea 400. 7. Din borcanul 3 transferam 300 in borcanul 1 care va avea 400.

Alex_capsunar • 2016-04-23 14:56

A doua pb, varianta americana // Notatii: A e cel care trece puntea in 5 minute, B e cel care o trece in 10 minute, C e cel care o trece in 20, iar D e cel care o trece in 25. Ideea rezolvarii: se castiga timp daca cei mai lenti, adica C si D, merg impreuna. Rezolvare: Trec puntea A si B (10 minute); Se intoarce A sa aduca lanterna (5 minute); Trec puntea C si D (25 de minute) {---> aici e cheia}; Se intoarce B sa aduca lanterna (10 minute); Trec puntea A si B (10 de minute). Total: 60 de minute. Alta solutie: Trec puntea A si B (10 minute); Se intoarce B sa aduca lanterna (10 minute); Trec puntea C si D (25 de minute); Se intoarce A sa aduca lanterna (5 minute); Trec puntea A si B (10 de minute). Total: 60 de minute.

Danutz Nastase • 2016-04-23 14:59

Problema cu borcanele // Problema cu borcanele e de dificultate medie, aș zice de nota 2 din 5. Important e să găsești o metodă de a rămâne cu 100 de mililitri în borcanul mare, fiindcă ai deja un borcan de 300 și dacă adaugi și 300 de mililitri de apă la 100 ai rezolvat problema. Cum facem: umplem borcanul de 500 de mililitri, apoi cu apa din borcanul de 500 îl umplem pe cel de 300. Rămânem cu 200 de mililitri în borcanul de 500. Vărsăm cei 300 de mililitri din borcanul mic în cel de 800, unde avem acum 600 de mililitri. Apoi pe cei 200 de mililitri rămași în borcanul de 500 îi punem în cel de 300. Vărsăm apa din borcanul de 800 în cel de 500 și aproape am rezolvat problema: în borcanul de 800 avem acum 100 de mililitri, în cel de 300 avem 200 de mililitri, iar cel de 500 e plin. Acum trebuie doar să vărsăm din borcanul de 500 cantitatea necesară pentru a-l umple pe cel de 300, unde sunt deja 200 de mililitri. Astfel, în borcanul de 500 mai rămânem cu 400 de mililitri, în cel de 800 avem 100 de mililitri, iar cel de 300 e plin. Ca să rezolvăm problema mai trebuie doar să golim borcanul de 300 în cel de 800 și avem două borcane cu câte 400 de mililitri: pe cel de 500 și pe cel de 800.

Dănutz Năstase • 2016-04-23 15:05

Răspunsurile la problemel cu traversările // Cred că dificultatea celorlaltor două probleme este tot de 2 din 5. La aceste probleme principiul de rezolvare este asemănător: ca să câștigi timp, trebuie să faci în așa fel încât puntea să fie traversată concomitent de cei 2 cei mai lenți oameni, astfel încât perioadele lor de traversare să nu se adune. Prin urmare, cei mai rapizi doi vor traversa împreună, iar cel mai rapid se va întoarce cu lanterna la cei mai lenți doi. Apoi vor traversa cei mai lenți doi și se va întoarce cu lanterna cel rămas deja de la prima traversare. Cei mai rapizi doi se vor întoarce apoi împreună. Prin urmare, la problema cu Guguță vor traversa mai întâi cei mai rapizi doi, în două minute. Cel mai rapid se va întoarce într-un minut cu lanterna. Apoi vor trece ceilalți doi împreună în 8 minute. Va prelua lanterna cel rămas deja de la prima traversare și o va duce pe celălalt mal în două minute. Apoi cei mai rapizi doi vor traversa din nou în două minute. Timpul total de traversare va fi de 2+1+8+2+2=15 minute. La fel vor face și cei din problema americană. Timpul de traversare va fi de 10+5+25+10+10=60 de minute.

tropojo • 2016-04-23 15:37

Goguda // 800 500 300 1. 800 0 0 2. 300 500 0 3. 300 200 300 4. 600 200 0 5. 600 0 200 6. 100 500 200 7. 100 400 300 8. 400 400 0 Trecerea puntii Trec intai T5 si T10 = 10 minute Se intoarce T5 = 5 minute Trec T20 si T25 = 25 minute Se intoarce T10 = 10 minute Trec T5 si T10 = 10 minute Total = 10 + 5 + 25 + 10 + 10 = 60 minute Trecerea puntii cu Guguta Trece Guguta T1 si soata T2 = 2 minute Se intoarce Guguta = 1 minut Trec socrii T7 si T8 = 8 minute Se intoarce soata = 2 minute Trec Guguta T1 si soata T2 = 2 minute Total = 2 + 1 + 8 + 2 + 2 = 15 minute P.S. Descrierea problemei e cam incurcata: "Socrul lui Guguta poate trece puntea in 8 minute, iar el in 1. Soacra are nevoie de 7 minute, iar Guguta - de 2. Pot trece toti puntea in 15 minute?" Practic Guguta apare mentionat de 2 ori cu 2 timpi diferiti in timp ce sotia nu apare deloc. Grad de dificultate 2 din 5

marian ovidiu • 2016-04-23 16:16

Borcane si punte // Borcane: notatii pentru usurarea explicatiei: A pentru 800ml,B pentru 500ml si C pentru 500ml pasul 1: versi din A in B si din B in C (rezulta A cu 300, B cu 200 si C cu 300) pasul 2: versi C in A (rezulta A cu 600, B cu 200 si C gol) pasul 3: versi B in C (rezulta A cu 600, B cu 0 si C cu 200) pasul 4: versi A in B( rezulta A cu 100, B cu 500 si C cu 200) pasul 5: Versi din B in C pana se umple mai are nevoie de 100 (rezulta A cu 100, B cu 400 si C cu 300) pasul 6: versi C in A si ai rezolvat problema (ai in A 400 si in B 400) Goguta si puntea: Solutia pleaca de la o ipoteza simpla: Felinarul trebuie sa fie la una din persoanele care trec puntea dar nu se specifica faptul ca ele trebuie sa stea alaturi. Asadar, Goguta pleaca in acelasi timp cu socrul (felinarul la socru). El a ajuns dincolo dupa 1 minut, socrul mai are 7minute. Cand Goguta ajunge dincolo, incepe traversarea soacra, care va ajunge dincolo in acelasi timp cu socrul. 8 minute pana aici. Goguta trece inapoi singur-cu felinarul (+1 minut), apoi da felinarul nevestei si incep trecerea inapoi . El termina intr-un minut iar nevasta in doua (+2 minute). Solutia este ca pot trece puntea in 11 minute.. As nota problemele cu 2 (ambele)

Mircea Lutic • 2016-04-23 16:58

Abordarea mea // Abordarea mea la prima problema a fost urmatoarea. Am notat fiecare stare cu 3 cifre indicand cate sute de ml sunt in borcanul mic, mediu si mare in aceasta ordine. Asta inseamna ca pornim de la 008 si vrem sa ajungem la 044. Avem doar doua operatii: golire si umplere astfel incat starile in care nu exista nici un borcan gol si nici unul plin sunt inaccesibile. Pornind de la coada (044) si explorand posibilitatile am gasit urmatoarele 2 solutii: 008, 053, 323, 026, 206, 251, 341, 044 008, 305, 035, 332, 152, 107, 017, 314, 044 Prima solutie are 7 miscari iar a 2a 8. Pentru a 2a problema cred ca e optim cand se intorc doar cei mai rapizi si cei mai lenti merg impreuna. Astfel: 2s: T1+T2 dus 1s: T1 intors 8s: T7+T8 dus 2s: T2 intors 2s: T1+T2 dus ========= 15s

NL • 2016-04-24 02:56

Comment sters de user // None

xvlad • 2016-04-24 11:52

Solutii // Borcane: 800 500 300 1. 300 500 0 2. 300 200 300 3. 600 200 0 4. 600 0 200 5. 100 500 200 6. 100 400 300 7. 400 400 0 Total: 7 vanturari. Dificultate: 2/5 Goguta si puntea: Trec: 1. Goguta + Guguta - dus = 2 min 2. Goguta - intors = 1 min 3. Socrii - dus = 8 min 4. Goguta - intors = 2 min 5. Goguta + Goguta - duc = 2 min Total: 2+1+8+2+2=15 min Dificultate: 2/5 Atletii si fricosii: Rezolvarea este similara: trec cei mai rapizi doi (10 min), se intoarce cel mai rapid singur (5 min), apoi trec cei mai fricosi doi (25 min), se intoarce al doilea cel mai rapid (10 min), apoi trec din nou cei mai rapizi doi (10 min). Timp total: 10 + 5 + 25 +10 +10 = 60 min. Dificultate: 2/5

Claudiu • 2016-04-24 18:19

Rezolvare problema punte // Rezolvare pentru problema cu puntea: 1. In prima etapa trece Goguta + Gogut, timpul fiind de 2 min. 2. Gogut se intoarce cu felinarul, in total 3 minute. 3. Trece Socrul cu Soacra, inca 8 min (11 in total). 4. Se intoarge Goguta, 13 min in total. 5. Trece Goguta cu Gogut, 15 min in total.

Marvin Popper • 2016-04-24 18:57

11 minute // Pornind de la restrictiile exprimate ale problemei, si anume: a. la orice moment tre sa fie 2 persoane pe punte si b. una din ele trebuie sa aiba felinarul, si considerand ca nu s-a zis nicaieri ca trebuie sa mearga impreuna, sugerez urmatoarea rezolvare care, recunosc, cam forteaza logica problemei: 1. Minutul 0 - socrii pleaca impreuna, socrul tinand felinarul, si fiecare merge cat de repede poate 2. Minutul 7 - soacra ajunge si ii striga lui Guguta (sau Guguta are ceas si stie precis cat de repede merge soacra-sa, pesemne inainte de casatorie asa stia cat timp are cu nevasta-sa in hambar pana se trezea cu maica-sa la usa); asadar Guguta porneste; pe punte sunt 2 persoane si una din ele are felinarul, iar Guguta are night vision 3. Minutul 8 - socrul si Guguta ajung la capat, Guguta ia felinarul si o ia inapoi 4. Minutul 9 - Guguta ajunge pe mal sursa si o ia pe nevasta-sa 5. Minutul 11 - Guguta si nevasta ajung pe malul destinatie Evident, solutia merge numai daca presupunem ca Guguta fie are night-vision, fie felinarul bate pana la el. Insa respecta restrictiile din textul problemei.

CetateanLogat • 2016-04-24 23:30

Problema cu borcanele - Partea 1 // Se cere ca problema sa fie rezolvata astfel incat sa nu se "vanture prea mult" ciorba. Din acesta cauza, trebuie sa fim siguri ca varianta aleasa este cea corecta. Din fericire, se poate arata ca exista doar doua posibile rezolvari, asa ca putem sa o alegem usor pe cea optima. Pentru a usura rezolvarea: a. Notam cele 3 borcane astfel: A - borcanul mare (800 ml capacitate) B - borcanul mijlociu (500 ml capacitate) C - borcanul mic (300 ml capacitate) b. Optional, ne imaginam ca cele 3 borcane se afla in varfurile unui triunghi echilateral cu baza BC (de la stanga la dreapta). c. Vom numi prescurtat fiecare turnare de ciorba dintr-un borcan in altul "manevra", si o vom reprezenta grafic printr-o sageata. De ex.: A-->B (500) => [A=300, B=500, C=0] inseamna ca turnam 500 ml din borcanul A in borcanul B iar in urma manevrei vom avea 300 ml in borcanul A, 500 ml in borcanul B si 0 ml in borcanul C. d. Pentru a alege varianta care "vantura" cel mai putin ciorba, sunt interzise urmatoarele manevre: i1 (interdictia 1) - manevra care reface configuratia anterioara. De ex., daca am turnat 500 ml din A in B, manevra urmatoare nu poate sa fie cea in care turnam inapoi cei 500 ml din B in A. i2 (interdictia 2) - manevra care produce o configuratie care putea sa fie obtinuta printr-un numar mai redus de manevre (numarate de la inceput). e. O manevra PRECISA inseamna turnarea intregului continut dintr-un borcan SAU umplerea completa a borcanului in care se toarna (in functie de situatie). Excludem varianta cu inclinarea borcanului (pentru a turna jumatate din continutul sau) deoarece aceasta manevra este imprecisa. Rezolvare: Exista doar 3 variante posibile care nu incalca i1 (interdictia 1) pentru secventa initiala de 2 manevre: I. A->B (500) urmata de B->C (300) II. A->C (300) urmata de C->B (300) III. A->B (500) urmata de A->C (300) Observam ca varianta III trebuie exclusa deoarece in aceasta varianta nu exista o manevra 3 care sa nu incalce i2 (interdictia 2).

CetateanLogat • 2016-04-24 23:33

Problema cu borcanele - Partea 2 (continuare)) // Ori turnam inapoi 500 ml din B in A, ori turnam inapoi 300 ml din C in A, configuratia obtinuta dupa 3 manevre ar fi putut sa fie obtinuta cu o singura manevra initiala. Raman de analizat doar variantele I. si II. Varianta I: Initial avem [A=800, B=0, C=0] 1. A->B (500) => [A=300, B=500, C=0] 2. B->C (300) => [A=300, B=200, C=300] 3. Singura varianta posibila care nu incalca i1 si i2 este: C->A (300) => [A=600, B=200, C=0] 4. Singura varianta posibila care nu incalca i1 si i2 este: B->C (200) => [A=600, B=0, C=200] 5. Singura varianta posibila care nu incalca i1 si i2 este: A->B (500) => [A=100, B=500, C=200] 6. Singura varianta posibila care nu incalca i1 si i2 este: B->C (100) => [A=100, B=400, C=300] 7. Singura varianta posibila care nu incalca i1 si i2 este: C->A (300) => [A=400, B=400, C=0] In acest moment problema este rezolvata, avem 400 ml in borcanul A si 400 ml in borcanul B. Am avut nevoie de 7 manevre in care s-au "vanturat" 2.200 ml de ciorba. *** Varianta II: Initial avem [A=800, B=0, C=0] 1. A->C (300) => [A=500, B=0, C=300] 2. C-> B (300) => [A=500, B=300, C=0] 3. Singura varianta posibila care nu incalca i1 si i2 este: A->C (300) => [A=200, B=300, C=300] 4. Singura varianta posibila care nu incalca i1 si i2 este: C->B (200) => [A=200, B=500, C=100] 5. Singura varianta posibila care nu incalca i1 si i2 este: B->A (500) => [A=700, B=0, C=100] 6. Singura varianta posibila care nu incalca i1 si i2 este: C->B (100) => [A=700, B=100, C=0] 7. Singura varianta posibila care nu incalca i1 si i2 este: A->C (300) => [A=400, B=100, C=300] 8. Singura varianta posibila care nu incalca i1 si i2 este: C->B (300) => [A=400, B=400, C=0] In acest moment problema este rezolvata, avem 400 ml in borcanul A si 400 ml in borcanul B. Am avut nevoie de 8 manevre in care s-au "vanturat" 2.300 ml de ciorba. Rezulta ca "Varianta I" este solutia corecta a problemei borcanelor.

CetateanLogat • 2016-04-24 23:36

Problema cu puntea ingusta // Pentru a reduce la minimum timpul necesar traversarii, este nevoie ca persoanele care se misca cel mai lent sa faca traversarea impreuna si o singura data (inainte), iar persoanele care se misca cel mai repede sa returneze lanterna (inapoi). Varianta I Facem urmatoarele notatii: Guguta (timp de traversare - 1 minut) = T1 Sotia (timp de traversare - 2 minute) = T2 Soacra (timp de traversare - 7 minute) = T7 Socrul (timp de traversare - 8 minute) = T8 Rezolvare: T1+T2 inainte (2 minute) T1 inapoi cu lanterna (1 minut) T7+T8 inainte (8 minute) T2 inapoi cu lanterna (2 minut) T1+T2 inainte (2 minute) Total - 2+1+8+2+2=15 minute *** Varianta II Facem urmatoarele notatii: T5 = timp de traversare - 5 minute T10 = timp de traversare - 10 minute T20 = timp de traversare - 20 minute T25 = timp de traversare - 25 minute Rezolvare: T5+T10 inainte (10 minute) T5 inapoi cu lanterna (5 minut) T20+T25 inainte (25 minute) T10 inapoi cu lanterna (10 minut) T5+T10 inainte (10 minute) Total - 10+5+25+10+10=60 minute

ADAUGĂ COMENTARIU (16 comentarii)

O singură inimă și 8 diagnostice puse unui făt, în burtica mamei. Dr. Răzvan Stanca, MedLife: „Cu ajutorul ecografului Voluson Expert 22 reușim să...

Recunoaștere internațională pentru programul gratuit dezvoltat de MedLife pentru testarea genetică a copiilor cu cancer

Testare genetică gratuită în cadrul programului #SperanțaNuMoareDeCancer

Cum pot fi crescute șansele de răspuns la tratament în cazul copiilor cu cancer? Specialiștii MedLife îți explică beneficiile testării genetice

INTERVIURILE HotNews.ro

01:30 • ACTUALITATE

Întors de la Moscova, ÎPS Vladimir le cere preoților moldoveni să se „pocăiască” și să revină la mitropolia aflată în slujba Rusiei: „Renunțați la orgolii, reveniți la starea de odinioară”

00:56 • ACTUALITATE

Slovacia: Guvernul lui Robert Fico lichidează televiziunea publică şi creează alta

00:39 • ACTUALITATE

Violență, lipsă de profesori și școli dărăpănate în Germania. Rezultatele barometrului școlar 2024 al Fundației Robert Bosch

00:21 • REVISTA PRESEI

Ciolacu: O să-mi cer scuze cred că de acum toată viaţa la domnul doctor Cîrstoiu

00:03 • SPORT

Premier League: Liverpool, înfrângere surprinzătoare în fața lui Everton – Pas greșit în lupta la titlu

Ieri • ACTUALITATE

Ilan Şor vrea federalizarea Republicii Moldova, iar limba țării să fie rusa. „Transnistria va fi de acord, în condițiile în care Rusia va fi mediator”

Ieri • SPORT

WTA Madrid: Fostă lideră mondială, eliminată în primul tur – Rezultatele zilei

Ieri • ACTUALITATE

Netanyahu califică drept „oribile” demonstrațiile pro-Gaza din campusurile americane

Ieri • SPORT

Antrenorul care o va pregăti pe FC Barcelona în sezonul viitor

Ieri • REVISTA PRESEI

Marcel Ciolacu: „Nu se rupe, dom'le, nicio coaliţie. Categoric! Suntem mai puternici decât niciodată”

Ieri • ACTUALITATE

Statele Unite au trimis în secret Ucrainei rachete cu rază lungă ATACMS / Kievul le-ar fi folosit deja

Ieri • ACTUALITATE

Schimbările sociale și nu violența ar putea explica scăderea diversității genetice masculine în perioada neolitică

Ieri • SPORT

VIDEO Liga 2: Prima echipă promovată matematic în SuperLigă - Sărbătoare în stilul lui Inter Milano

Ieri • ACTUALITATE

Schimbări majore la pașaportul simplu electronic: Va putea fi livrat prin curier la orice adresă din țară, iar costul expedierii va fi inclus în preț

Ieri • ACTUALITATE

Adolescent arestat în Franța, după ce a spus că vrea să moară ca un „martir” la Jocurile Olimpice

Facem România Bine

Insurtech Talks

Pagini de [cod]

Medicină extraordinară

Banking și mai și

Memorial - Spitalul din afară

Sistemul Garantie-Returnare

Blogul PwC România

EY - Fiscalitatea la zi

Porțile ni se deschid

INVESTIGAȚIE Banii big farma ajung la societatea medicală condusă de ministrul Rafila prin firma unui fost șef al spitalului SRI

LIVE Război în Ucraina - ziua 791: Biden promulgă pachetul de ajutor, SUA vor începe să trimită armament / Britanicii trimit un „cadou” special aviației ucrainene / Venituri duble din petrol și gaze în aprilie pentru Rusia

Medic român întors din Franța: „Mă întreb câți medici există în Europa atât de bogați precum dr. Cîrstoiu. Doctori buni pleacă scârbiți în străinătate”

FOTO România, afectată de un val intens de praf saharian / Imagini cu mașini acoperite de praf în București - VIDEO

VIDEO Primarul Radu Mihaiu: „Să-și cumpere câte mașini vrea, însă nu e responsabilitatea statului să-i asigure loc de parcare pentru fiecare mașină”

Ciolacu îl roagă pe „prietenul” Piedone să se retragă din cursa pentru Capitală / Ce-i răspunde candidatul PUSL

EXCLUSIV. Directivă PNL pentru toți șefii din județe: Solicitați respingerea Alianței AUR la Birourile electorale! / Ce au descoperit

TikTok își suspendă recompensele în UE fiind acuzată că încurajează dependența

Finanțări „Femeia Antreprenor” 2024: Noua grilă de punctaj elimină criteriile restrictive cu incubatoare de afaceri și brevete. Când încep înscrierile la granturile de 200.000 lei

Prima acțiune a statului român împotriva giganților Shein și Temu. Mergem pe urmele francezilor și lovim fenomenul fast fashion?

25 de ani de DENT ESTET în România -Investiții de zeci de milioane de euro în infrastructură medicală și sute de mii de pacienți din țară și străinătate tratați la standarde internaționale

Grindeanu despre salvarea Tarom: „Decizii care nu sunt foarte aplaudate, dar absolut necesare”

3 femei diferite, 3 povești unice, o singură constantă – Regina Maria și călătoria spre maternitate

„Nu mai puteam să ridic mâna, nu mai puteam să fac nimic.” Problemele „crunte” ale unei tinere mame, rezolvate prin terapia durerii

Pacient cu cancer de colon în stadiu avansat, operat de dr. Decebal Fodor de la Spitalul Regina Maria Brașov. Fără colostomă, fără recidive și cu analize perfecte!

Iulian Comanescu

Țăranii istoriei, orășenii Orientului

Mircea Morariu

Calendare

Cristian Felea

Viitorul (inconturnabil) pe care îl trăim

Vladimir Tismaneanu

Antinomiile radicalismului utopic

Dan Alexandru Chiță

Școala – divertisment și elite

O nouă listă de ambalaje interzise în UE, inclusiv în România, din 2030 (Parlamentul European)

Joburi în IT: Compania-mamă a Mega Image caută 250 de specialiști în tehnologie, pentru un hub tech la București

Finanțări „Femeia Antreprenor” 2024: Noua grilă de punctaj elimină criteriile restrictive cu incubatoare de afaceri și brevete. Când încep înscrierile la granturile de 200.000 lei

Aplicația românească Star Taxi se extinde în încă 4 orașe

ANIS, asociația care reunește patronii din IT, are un nou președinte

UE adoptă noi norme privind încălcarea regulilor de circulație în străinătate

Parlamentul European adoptă noi norme pentru a reduce, refolosi și recicla ambalajele

Ciolacu se face acum că nu-l cunoaște pe Ion Doldurea, tatăl patronului stației GPL de la Crevedia

Câți bani investește China în Ungaria

Schimbarea climatică aduce schimbări și în turism

Provocarea de logica a saptamanii: Guguta, ciorba si puntea afurisita (UPDATE cu rezolvarile)

INVESTIGAȚIE Banii big farma ajung la societatea medicală condusă de ministrul Rafila prin firma unui fost șef al spitalului SRI

VIDEO Primarul Radu Mihaiu: „Să-și cumpere câte mașini vrea, însă nu e responsabilitatea statului să-i asigure loc de parcare pentru fiecare mașină”

fanatik.ro: Deținutul periculos care a evadat la începutul lunii aprilie, bătut în închisoare. Agresorul a fost achitat

Programul Școala de Bani din Bibliotecă: peste 4.300 de copii și adulți au învățat, în ultimul an, despre bani prin intermediul a 90 de...

lovedeco.ro: De la oraș la sat: un tată și fiica lui au renovat o casă șubredă și o șură veche de 100 ani

EXCLUSIV. Directivă PNL pentru toți șefii din județe: Solicitați respingerea Alianței AUR la Birourile electorale! / Ce au descoperit

Medic român întors din Franța: „Mă întreb câți medici există în Europa atât de bogați precum dr. Cîrstoiu. Doctori buni pleacă scârbiți în străinătate”

Marea Britanie va trimite un „cadou” special forțelor aeriene ucrainene / Ce se știe despre Paveway, o armă de ultimă generație - VIDEO

panorama.ro: „Gângăniile” electronice fără care nu ai avea telefon, mașină sau televizor. Cum arată piața de sute de miliarde de dolari care învârte lumea

smartliving.ro: Testul care îți arată cât de rezistent e creierul tău. Neurochirurg: „Este o paradigmă revoluționară în domeniul sănătății...

De ce grecii și spaniolii îi invidiază pe români pentru viteza internetului

„Poligon militar, loc de gunoaie și casă a migranților” - mesajul lui Șor, de la Moscova, contra referendumului Moldovei pentru UE. Analist: „Sunt...

Intra în contul tau folosind adresa de e-mail si parola

Creaza un cont nou pe HotNews.ro

O singură inimă și 8 diagnostice puse unui făt, în burtica mamei. Dr. Răzvan Stanca, MedLife: „Cu ajutorul ecografului Voluson Expert 22 reușim să...

Recunoaștere internațională pentru programul gratuit dezvoltat de MedLife pentru testarea genetică a copiilor cu cancer

Cum pot fi crescute șansele de răspuns la tratament în cazul copiilor cu cancer? Specialiștii MedLife îți explică beneficiile testării genetice

Întors de la Moscova, ÎPS Vladimir le cere preoților moldoveni să se „pocăiască” și să revină la mitropolia aflată în slujba Rusiei: „Renunțați la orgolii, reveniți la starea de odinioară”

Slovacia: Guvernul lui Robert Fico lichidează televiziunea publică şi creează alta

Violență, lipsă de profesori și școli dărăpănate în Germania. Rezultatele barometrului școlar 2024 al Fundației Robert Bosch

Ciolacu: O să-mi cer scuze cred că de acum toată viaţa la domnul doctor Cîrstoiu

Premier League: Liverpool, înfrângere surprinzătoare în fața lui Everton – Pas greșit în lupta la titlu

Ilan Şor vrea federalizarea Republicii Moldova, iar limba țării să fie rusa. „Transnistria va fi de acord, în condițiile în care Rusia va fi mediator”

WTA Madrid: Fostă lideră mondială, eliminată în primul tur – Rezultatele zilei

Netanyahu califică drept „oribile” demonstrațiile pro-Gaza din campusurile americane

Antrenorul care o va pregăti pe FC Barcelona în sezonul viitor

Marcel Ciolacu: „Nu se rupe, dom'le, nicio coaliţie. Categoric! Suntem mai puternici decât niciodată”

Statele Unite au trimis în secret Ucrainei rachete cu rază lungă ATACMS / Kievul le-ar fi folosit deja

Schimbările sociale și nu violența ar putea explica scăderea diversității genetice masculine în perioada neolitică

VIDEO Liga 2: Prima echipă promovată matematic în SuperLigă - Sărbătoare în stilul lui Inter Milano

Schimbări majore la pașaportul simplu electronic: Va putea fi livrat prin curier la orice adresă din țară, iar costul expedierii va fi inclus în preț

Adolescent arestat în Franța, după ce a spus că vrea să moară ca un „martir” la Jocurile Olimpice

INVESTIGAȚIE Banii big farma ajung la societatea medicală condusă de ministrul Rafila prin firma unui fost șef al spitalului SRI

LIVE Război în Ucraina - ziua 791: Biden promulgă pachetul de ajutor, SUA vor începe să trimită armament / Britanicii trimit un „cadou” special aviației ucrainene / Venituri duble din petrol și gaze în aprilie pentru Rusia

Medic român întors din Franța: „Mă întreb câți medici există în Europa atât de bogați precum dr. Cîrstoiu. Doctori buni pleacă scârbiți în străinătate”

FOTO România, afectată de un val intens de praf saharian / Imagini cu mașini acoperite de praf în București - VIDEO

VIDEO Primarul Radu Mihaiu: „Să-și cumpere câte mașini vrea, însă nu e responsabilitatea statului să-i asigure loc de parcare pentru fiecare mașină”

Ciolacu îl roagă pe „prietenul” Piedone să se retragă din cursa pentru Capitală / Ce-i răspunde candidatul PUSL

EXCLUSIV. Directivă PNL pentru toți șefii din județe: Solicitați respingerea Alianței AUR la Birourile electorale! / Ce au descoperit

TikTok își suspendă recompensele în UE fiind acuzată că încurajează dependența

Finanțări „Femeia Antreprenor” 2024: Noua grilă de punctaj elimină criteriile restrictive cu incubatoare de afaceri și brevete. Când încep înscrierile la granturile de 200.000 lei

Prima acțiune a statului român împotriva giganților Shein și Temu. Mergem pe urmele francezilor și lovim fenomenul fast fashion?

25 de ani de DENT ESTET în România -Investiții de zeci de milioane de euro în infrastructură medicală și sute de mii de pacienți din țară și străinătate tratați la standarde internaționale

Grindeanu despre salvarea Tarom: „Decizii care nu sunt foarte aplaudate, dar absolut necesare”

3 femei diferite, 3 povești unice, o singură constantă – Regina Maria și călătoria spre maternitate

„Nu mai puteam să ridic mâna, nu mai puteam să fac nimic.” Problemele „crunte” ale unei tinere mame, rezolvate prin terapia durerii

Pacient cu cancer de colon în stadiu avansat, operat de dr. Decebal Fodor de la Spitalul Regina Maria Brașov. Fără colostomă, fără recidive și cu analize perfecte!

Țăranii istoriei, orășenii Orientului

Calendare

Viitorul (inconturnabil) pe care îl trăim

Antinomiile radicalismului utopic

Școala – divertisment și elite

O nouă listă de ambalaje interzise în UE, inclusiv în România, din 2030 (Parlamentul European)

Joburi în IT: Compania-mamă a Mega Image caută 250 de specialiști în tehnologie, pentru un hub tech la București

Finanțări „Femeia Antreprenor” 2024: Noua grilă de punctaj elimină criteriile restrictive cu incubatoare de afaceri și brevete. Când încep înscrierile la granturile de 200.000 lei

Aplicația românească Star Taxi se extinde în încă 4 orașe

ANIS, asociația care reunește patronii din IT, are un nou președinte

UE adoptă noi norme privind încălcarea regulilor de circulație în străinătate

Parlamentul European adoptă noi norme pentru a reduce, refolosi și recicla ambalajele

Ciolacu se face acum că nu-l cunoaște pe Ion Doldurea, tatăl patronului stației GPL de la Crevedia

Câți bani investește China în Ungaria

Schimbarea climatică aduce schimbări și în turism