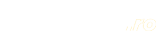Un melc a fost luat de furtună și a aterizat într-un puț adânc de 10 de metri. În fiecare zi parcurge doi metri spre gura puțului, dar noaptea adoarme și alunecă înapoi un metru. Câte zile îi trebuie ca să iasă din puț?

O muscă și un păianjen sunt într-o cutie ca cea din imagine, cu dimensiunile (10x4x4 cm). Ambele gângănii sunt rupte de oboseală. Musca s-a oprit să-și tragă sufletul în punctul B, care se află la jumătatea laturii. Păianjenul este în punctul A, aflat și el la jumătatea laturii. Care e cel mai scurt drum pe care păianjenul poate ajunge la muscă? (Bineînțeles, nu e Superpăianjenul, să arunce un fir și apoi să coboare pe el până la muscă - trebuie să meargă pe pereții cutiei.)
Mentiuni
Îi mulțumesc lui Mihai Negrea pentru verificări. I-aș ruga pe cei care îmi trimit rezolvări prin e-mail să spună și cât de grea li se pare problema la care răspund (pe o scară de la 1 la 5).
Mulțumesc. Comentariile, întrebările, propunerile, sugestiile și reclamațiile sunt așteptate la viorel.zaicu@hotnews.ro.
Rezolvări
Melcul
Nouă. Parcurge un metru în fiecare zi (atunci când măsurăm a doua zi dimineața), numai că în ziua a noua ajunge deja la gura puțului.
Musca
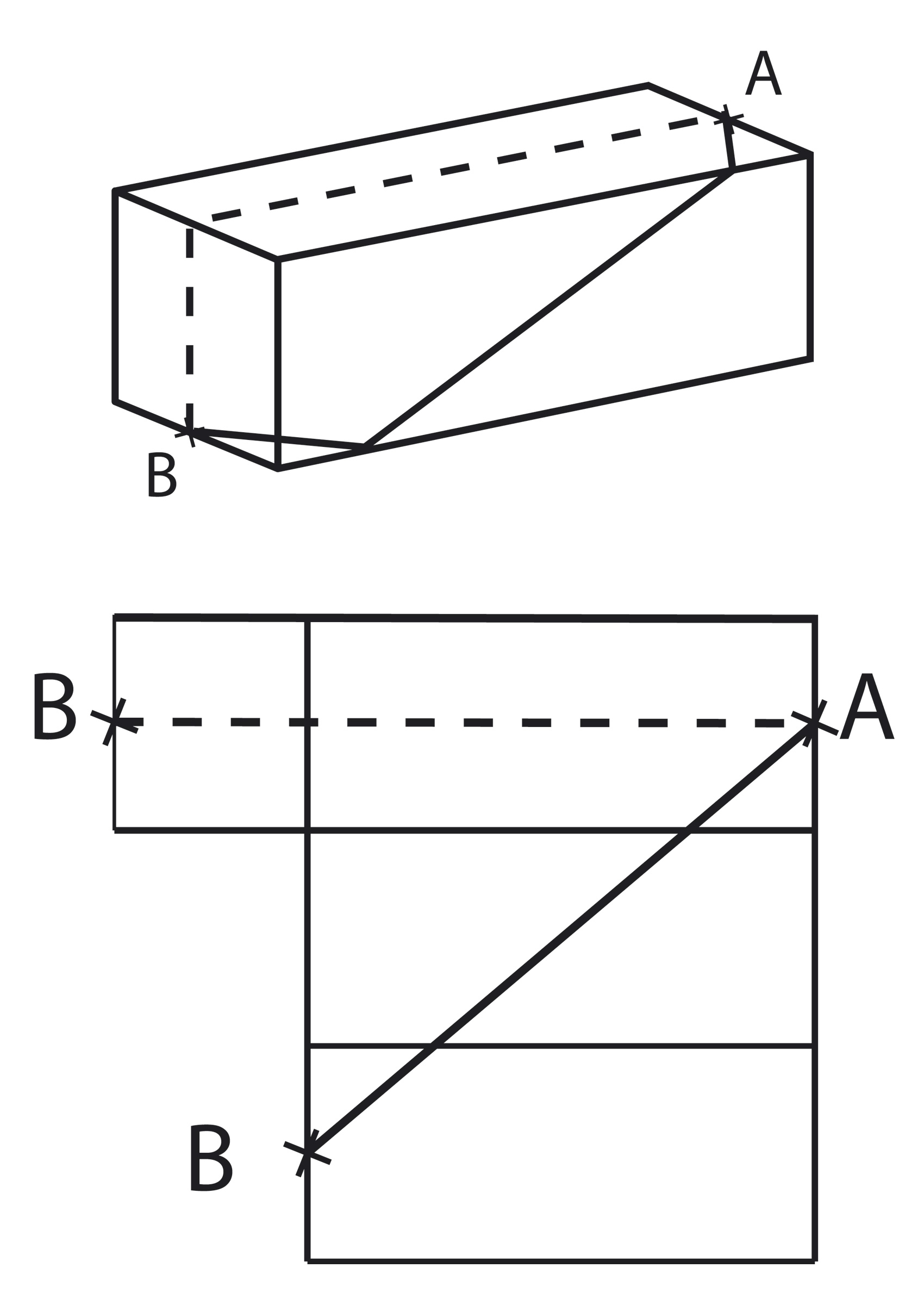
Multora li se pare paradoxal, însă drumul cel mai scurt nu este cel marcat aici de linia punctată, ci acela marcat de linia plină. Bineînțeles, cutia poate fi desfășurată în mai multe moduri, așa că mai există trasee, dintre care două sunt și ele cele mai scurte iar unul este... cel mai lung cu putință. Dacă vă distrați cu desfășurarea cutiei le puteți găsi foarte ușor.
Cititi si provocarile de logica din ultimele 11 saptamani:
Painea prajita si mancatorii de iaurt
Cinci cercuri si doisprezece infometati
Varstele copiilor si spargatorii